KS1 & KS2 maths: multiplication facts

Why cram children's heads with endless calculations, asks Mike Askew, when there are easier ways of getting to grips with multiplication fac

Learning multiplication and division facts needn’t be a long and laborious task. Armed with a toolkit of mental strategies, children can figure out all manner of calculations. Using these 10 techniques, you can help pupils to master their times tables without having to learn every line of arithmetic by rote.

1 Make connections

Chanting tables is only part of committing multiplication facts to memory. While the time tables are neat, they have the disadvantage of keeping calculations such as 6 x 7 and 7 x 6 separate. Often children who have learned up to the six times table do not realise they know much of the seven times table from the facts already covered. And while some pupils do enjoy chanting tables, many do not. Teaching the multiplication facts strategically helps children to make connections and reduces the burden on their memory.

2 Triple whammy

Make sure that children are secure in the knowledge of triples - the sets of three numbers linked together by multiplication and division, for example 3, 8, 24. They should know that 3 x 8 = 24, 8 x 3 = 24, 24 ÷ 3 = 8, 24 ÷ 8 = 3. A simple teaching aid for this is a set of triangular cards with number from a triple placed in each of the corners. Cover up one of the numbers and invite children to express the multiplicative relationship between the remaining two. 3 multiplied by what is 24? What is 24 divided by 3? and so forth.

3 The old switcheroo

Multiplication is commutative: the order of the numbers doesn’t affect the answer. For example, 3 x 4 is the same result as 4 x 3. This immediately reduces the number of multiplication facts to remember by almost half. An array model helps make this clear. Here, rotating the array by 90° shows that four rows of three is the same as three rows of four.

4 Start small

When adding, we encourage children to start with the larger number. For example, if still at the stage of counting on when adding 4 + 17, it’s easier to count on 4 from 17 than to count on 17 from 4. Children use skip-counting strategies when beginning with their tables and asked to calculate say, 7 x 3, will count 3, 6, 9, 12, 15, 18, 21. Drawing on the commutative property, we might take a lesson from Japanese pupils who are encouraged to put the smaller number first: instead of 7 x 3, calculate 3 x 7. Now you only have to count on 7, 14, 21. Nine times four? Don’t do that, do four times nine.

5 Double time

Knowledge of doubles is central to committing multiplication facts to memory. Being able to double doesn’t just give you the two times table - it also means you can quickly remind yourself what, say, 8 x 6 comes to if you’ve forgotten.

• Double six: 2 x 6 = 12
• Double again: 4 x 6 = 24
• Double again: 8 x 6 = 48

Arrays are again helpful models for showing why this works.

6 Starter for 10

Children need to be fluent in multiplying by 10 and later by 100. They might say that the shortcut method is to “add a zero”. However, this rule does not hold for multiplying decimal numbers so it is better to point out that multiplying by 10 makes everything 10 times bigger. Base 10 blocks are useful here: setting out, say, 24 as two 10- sticks and four units, each of these becomes 10 times bigger. Each 10 stick needs to be replaced by a 100 square, and each unit replaced by a 10 stick: 24 gets scaled up by a factor of 10 to become 240. The result is that all the digits move one place to the left.

7 The whole 9 yards

A way of exploring the nines pattern is to multiply by 10 and subtract the number being multiplied. So nine times four is forty minus four, that’s 36.

8 Hip to be square

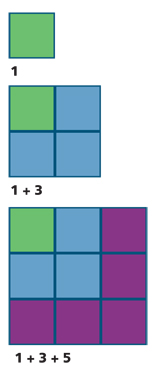The square numbers - 1 x 1, 2 x 2 up to 10 x 10 and beyond - are the cornerstones of the multiplication facts. If children know say, 6 x 6 = 36, they can easily work out 7 x 6 by adding on another 6 to get 42. Again, working with arrays and the pattern of how square numbers grow can help children commit these to memory.

1
1 + 3
1 + 3 + 5

9 Winning combinations

If children are confident with these strategies, they will become fluent with the multiplication and division facts up to 10 x 10. A bonus to this approach is that combining strategies allows them to work mentally beyond 10 x 10. For example, appreciating that doubling and doubling again is the same as multiplying by four makes 36 x 4 a reasonable mental calculation. Reversing this - halving and halving again - gives a useful strategy for mentally figuring out 76 divided by four. Combining doubling with multiplying by 10 makes mental multiplication by 20 possible. Figuring out 38 x 5 by halving 380 (38 x 10) is more efficient than multiplying the 30 and 8 x 5 separately.

10 What about the 7s and 8s tables?

Confident doublers will appreciate that multiplying by eight can be done by doubling, doubling and doubling again. If children know that multiplication is commutative, they can turn around most of the seven and eight times table facts - 7 x 5 becomes 5 x 7. Only three facts are then not covered in the other tables - 7 x 7, 8 x 8, and 7 x 8. The first two are covered by knowing the square numbers. Seven eights? Well, maybe you just have to remember that one - it’s a table fact that everyone finds most difficult to recall! Although you might note that 5, 6, 7, 8 can turn into 56 = 7 x 8.

Key strategies

6 Ways to take the grind out of learning the times tables…

• 2, 4 and 8 times tables: doubling
• 10 times table: place value
• 5 times table: skip counting in 5s and halving the 10 times table
• 3 times table: skip counting
• 6 times table: double the three times table
• 7 times table: commutativity

Play Bingo!

Children jot down eight numbers from 1 to 36 (or 1 - 100 if working with a 1-10 dice). Roll a dice twice to create a multiplication calculation. Players strike out the answer if it is one of their eight numbers. Which are good numbers to choose?

Good times

Play ‘fizz, buzz’ and help children rehearse the pattern of multiples…

Count around with everyone taking it in turns to say the next number. Count again, but instead of saying the multiples of five, children have to say “fizz”. Start again, this time saying “buzz” instead of the multiples of three. A challenge is to count around and say “fizz” for the multiples of five, and “buzz” for the multiples of three. What do you say instead of 15?

Mike Askew is Director of BEAM Education and Professor of Mathematics Education, King’s College, London

BEAM Education is a specialist publisher of mathematical books and resources, and provides training consultancy in mathematics education. They publish a range of more than 100 books, mathematical games and equipment. Visit http://www.beam.co.uk to find out more.