KS1 & KS2 Maths: addition and subtraction

Could the language you use to teach maths be hampering children’s progress? Mike Askew looks at the best way to discuss...

Key stage 1

There are several important concepts that link addition and subtraction in KS1. Children come to understand that addition can be done in any order, but subtraction as ‘take away’ cannot. However, when treating subtraction as ‘difference’, a pair of numbers can be compared in any order.

Children’s early experience of addition and subtraction are closely linked to everyday actions of adding or removing items to a collection. For example, a game involving rolling a dice and collecting the number of counters corresponding to the dice score can easily be recorded as a simple addition. So, a roll of five followed by a roll of three could be recorded as:

5 + 3 = 8

This can be extended by rolling two dice and talking about which order to add them in and whether it makes any difference to the total.

“I’ve rolled a four and a two. Let’s start with four and add on two. Four, five, six. Now you try starting with the two and adding on four.”

Modelling such calculations with counters or cubes can help children come to understand that it does not matter which order numbers are added in and that it is easier to start with the larger number.

It is a short step from situations where an initial quantity is made larger to one where a set of objects is made smaller by removing some. Again, a simple game might involve starting with a collection of, say, 10 items and rolling the dice to decide how many to put back in the pot. Unlike the introduction of the addition sign, I recommend not rushing to introduce the subtraction sign until children have had experience of subtraction as both ‘taking away’ and ‘difference’.

Why delay the introduction of the ‘minus sign’? Well, too much emphasis too soon on ‘reading’ 7 - 3 as ‘seven take away three’ can cause children to think this is the only meaning to attach to the minus symbol. Indeed, this is a default reading for most adults: ask someone to read out 2001 – 1997 and they are likely to use ‘take away’. Why is that a problem? If children ‘overlearn’ too soon that the minus symbol is ‘take away’, they can find if difficult to associate the same symbol with finding a difference. This can lead to them using ‘take away’ as their preferred strategy for carrying out a calculation, even when 2001 – 1997 is better off being treated as finding the difference.

To complement increasing and decreasing situations we need to provide children with experiences of ‘part-part-whole’ situations: that is contexts where everything is present the whole time – nothing is added or taken away – but the context can still be mathematically described in terms of addition or subtraction. Take this simple context for example:

Joe has a collection of eight t-shirts, five red and three yellow

This is a typical part-part-whole situation. There is a whole – eight t-shirts – made up of two distinct parts – red and yellow. Talking about the relationships between the parts and the whole leads to the language of difference as well as linking addition and subtraction. Consider presenting

Joe’s story in this form:

Joe has eight t-shirts, all either red or yellow. Five of his t-shirts are red. How many of his tshirts are yellow?

Children can solve this problem informally, using counters or drawings and the teaching skill is to help them record these with mathematical symbols. For example, a child may put out five red counters and add yellow ones until there is a total of eight. This is a missing addend situation (what needs to be added to five to make eight?) and can be recorded as:

5 + [ ] = 8

Another might draw eight t-shirts, colour five in red and count up the remaining three. This can be linked to talking about finding the difference between eight and five and recorded as:

8 - 5 = [ ]

Lower key stage 2

Children need lots of experience in choosing suitable number operations to solve a given problem, particularly when the ‘action’ of the problem may not suggest the most appropriate way to carry out the calculation. For example, consider this seemingly simple word problem:

Sally was a keen collector of postcards and had a collection 304. When she decided to take up collecting stamps instead, Sally gave away 297 of her postcards. How many postcards did she have left?

Here the ‘action’ of the problem is one of ‘giving away’, close to ‘taking away’ and implicitly suggesting that, literally, taking away 297 from 304 is the mathematics to do. However, mathematically, the solution is much easier to find through finding the difference between 304 and 297. A teaching strategy that I find helps here is to get children to record the mathematical sentence they think best represents a problem, but not to actually go on and figure out the solution. In this instance they might record the problem as:

304 - 297 = [ ]

297 + [ ] = 304

Talking these through with the class or group helps the children to understand that what we do mathematically may not always be the same as what is suggested by the ‘story’ of the problem.

Another understanding that needs to be worked on here is not being lulled into thinking that particular words in a problem provide the ‘clue’ to which operation to use. Look at this pair of problems:

• Russell had saved £27 towards buying a jacket. His gran gave him £35 more on this birthday. How much does Russell now have towards his jacket?

• Jennie had saved $27 towards a ticket for the theatre. The ticket costs $35. How much more does Jennie have to save towards her ticket?

The structure and wording of each problem is similar but the underlying mathematics is very different: addition in the first case and subtraction in the second. The second problem is further complicated by the fact that it could be solved as a missing addend problem – what needs to be added to 27 to make 35? Or as difference calculation: 35 - 27. Too often these subtle complexities pass children by and they focus simply on the fact that both problems contain the word ‘more’ and echoes someone having once told them that ‘more’ means ‘add’ and so they add in each case. Once children start out on this route, it is difficult to break them out of it: the fact that sometimes ‘more’ actually does mean ‘add’ means they are sometimes correct and a partial reward system is set up (sometimes getting the reward of getting it right).

Getting the children to create simple diagrams of the elements of the problem can help them sort out their thinking. They sketch out the information in the problem and then use this to create an image of what they are trying to find, as illustrated below.

Upper key stage 2

Playing around with one or two calculations and modelling these on an open number line can help children develop further their understanding of the relationship between addition and subtraction and deepen their mental mathematics.

Consider a calculation like 637 - 389 and the different ways that this can be modelled on an open number line.

We could start with 637 marked towards the right hand end of a line. Taking away is modelled by jumping back 389 on the line. Children doing this will usually start by jumping back by the largest amount, 300, then the 80 and then the 9.

The beauty of the open number line is the potential it has for other, possibly more efficient, strategies to be explored. For example, noticing that 389 is close to 400, we could subtract the 400 and then ‘compensate’ for the fact that we took away more than we needed to.

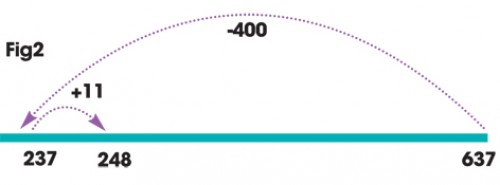
We can also model finding the difference on the number line. Now, rather than marking 637 and jumping back, we mark both numbers on the line and figure out the size of the difference between them. We can do this by counting up from the smaller number to the larger.

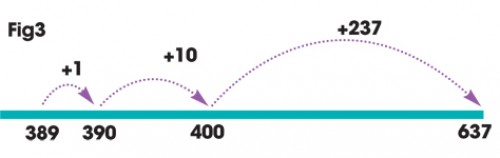
Here again the number line lends itself to playing with the numbers. Now attending to the fact that 389 is close to 390, we might add 1 to each number, keeping the difference between them constant: a method known as – hardly surprisingly – constant difference.

We can make things even easier by adding a further 10 to each number.

Now all we have to do is find the difference between 300 and 648 – that’s easy, 348.

These models for carrying out subtraction on the number line lend themselves to becoming mental methods.

‘648 subtract 289.Well I can take away 300, that’s 348 but that’s 11 more than I need to take way, so eleven onto 348 is 359.’

Or

‘648 subtract 289. What’s the difference between these two? Making 289 up to 300 means adding 11 to it. Adding 11 to 648 will preserve the difference. So that’s 659. The difference between 659 and 300 is 369.’

If I get lost in the mental reasoning, a quick sketch can extend the mental screen.